Introduzimos aqui o curso de Fundamentos do Eletromagnetismo, ou o Curso de Física III como é denominado em várias unidades de ensino de cursos superiores. A lista de exercícios encontra-se no final deste post.
A Lei de Coulomb trata das forças de interação elétrica entre cargas elétricas puntuais.
Este post contará com notas de aulas, vídeo aulas e proposta de exercícios, e como bibliografia básica utilizaremos o livro texto:
Halliday, David, 1916-2010 Fundamentos de física, volume 2 : gravitação, ondas e termodinâmica / David Halliday , Robert Resnick , Jearl Walker ; tradução Ronaldo Sérgio de Biasi. – 10. ed. – Rio de Janeiro : LTC, 2016.
Ao final do post encontra-se um espaço para comentários, críticas e sugestões.
A disciplina de Fundamentos do Eletromagnetismo, aqui denominada Física III, é composta por uma série de conteúdos ministrados nos cursos com duração de um semestre nas várias instituições de ensino superior do Brasil. A bibliografia aqui adotada apresenta a teoria em 12 capítulos
Uma peculiaridade da Física III é a impossibilidade de assimilação dos conteúdos estudando capítulos independentes, ou seja, é praticamente impossível assimilar o conteúdo referente a Potencial Elétrico sem ter assimilado o assunto que trata de Campo Elétrico.
A Lei de Coulomb
A expressão matemática da Lei de Coulomb é
(1) ![]()
Ou ainda, na forma vetorial
(2) ![]()
Sendo ![]() a força elétrica que a carga
a força elétrica que a carga ![]() exerce sobre
exerce sobre ![]() e
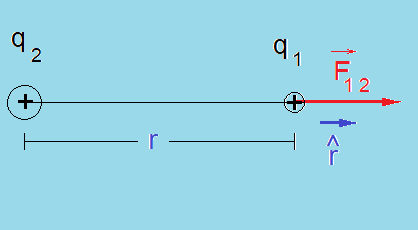
e ![]() a distância que separa as duas cargas, centro a centro conforme mostra a figura abaixo.
a distância que separa as duas cargas, centro a centro conforme mostra a figura abaixo.
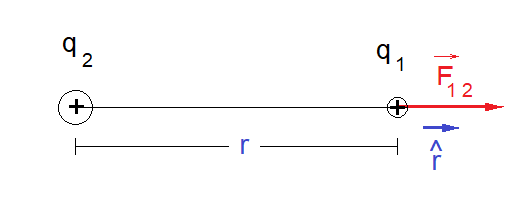
Lei de Coulomb – Conceitos Iniciais
Lei de Coulomb e o Princípio da Superposição
Quando temos a interação de várias cargas e precisamos determinar, por exemplo, a força que um conjunto de cargas exerce numa carga específica, utilizamos o princípio de superposição.
Um Problema completo sobre Cargas Puntuais
Lista de Exercícios sobre Lei de Coulomb
A lista de exercícios sobre Lei de Coulomb encontra-se na janela abaixo. Nunca avance para a próximo assunto sem resolver um número razoável de exercícios do assunto atual.







![Rendered by QuickLaTeX.com \[V=\frac{\lambda}{4\pi \varepsilon _0}\,ln\,\left(\frac{x}{z}+ \frac{\sqrt{x^2+z^2}}{z} \right) \Big|_{x=0}^{x=L}\]](https://fismat.com.br/wp-content/ql-cache/quicklatex.com-5815660df4a623c9b8d01619dbc52413_l3.png)

