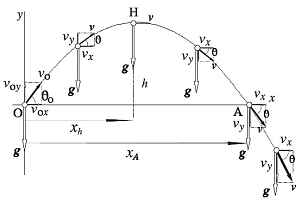
Análise de Gráficos na Cinemática
Através de um gráfico é possível resumir uma teoria, ou o acontecimento de um determinado evento da natureza. Na Física não é diferente; analisando um diagrama é possível retirar várias informações de um fenômeno físico. Mas para entender o que um gráfico está ilustrando é necessário saber fazer a sua leitura . Nesse momento estamos interessados a aprender como um problema da cinemática pode ser expressado através de um gráfico.
Função Constante e Função de 1º Grau na Cinemática
A aula do vídeo a seguir, mostra como a função constante e a função de 1º grau retrata alguns problemas de cinemática. Aprender fazer a leitura desses gráficos, servirá, inclusive, como base para outros assuntos da Física que serão vistos a seguir.
Função Horária da Posição no Movimento Uniformemente Variado
O movimento uniformemente variado, se caracteriza pela aceleração constante. A descrição física deste tipo de movimento nos permitirá entender uma série de problemas de interesse, como, o movimento de uma carga elétrica no interior dos tubos de raios catódicos, que até pouco tempo eram usados nos aparelhos de TV em nossos lares, e que ainda hoje são utilizados nos hospitais e em laboratórios de pesquisas. Entender os fundamentos físicos e matemáticos deste tipo de movimento vai permitir entender e descrever movimentos mais complexos e de interesse da humanidade. O movimento uniformemente variado descreve muito bem o movimento de objetos próximos à superfície da Terra, quando a resistência do ar pode ser ignorada.
O vídeo a seguir mostra atividades de aprendizagem sobre função horária das posições no movimento uniformemente variado .
Cinemática: Conceitos Iniciais
A Cinemática é o ramo da Física que estuda o movimento sem levar em conta as causas desse movimento. Existem um grande quantidade de problemas, acontecimentos, e aplicações aplicações tecnológicas de interesse nos quais as cinemática está presente. O simples fato de atravessar a rua de uma grande cidade exige que você “resolva” um problema de cinemática. Note que você observa a velocidade do carro que vem seguindo em sua direção, observa também a largura da rua, além de avaliar sua capacidade física que lhe garante uma rápida travessia, e decide se pode ou não atravessar. Quando os astrônomos fazem previsão de uma chuva de meteoros que se aproximam de nosso planeta, os conceitos de cinemática estão presentes nos cálculos realizados para fazer esta previsão.
Poderíamos citar aqui, centenas de aplicações da cinemática, mas ao invés disso, serão apresentados abaixo, uma série de vídeo aulas com o objetivo de mostrar os conceitos básicos da cinemática. Os vídeos a seguir apresentam-se na ordem mais conveniente para sua aprendizagem.
Conceitos Básicos de Cinemática
Conhecer os conceitos básicos de cinemática é de grande importância para que você possa dar seguimento ao curso de Física do Ensino Médio. No vídeo a seguir vamos apresentar os conceitos gerais sobre referencial , repouso , movimento e trajetória .
Velocidade Escalar Média e Velocidade Instantânea
Depois de aprender os conceitos básicos de cinemática, passaremos agora a tratar do conceito de velocidade velocidade escalar média e velocidade instantânea. É interessante que você comece a tomar notas dos conceitos estudados. Para isso adquira o hábito de fazer sempre uma síntese do que foi estudado.
Movimento Uniforme: Equação Horária das Posições
A aula mostrada no vídeo anterior tratou de velocidade média e velocidade instantânea. Quando a velocidade média é igual a velocidade instantânea, o movimento é denominado Movimento Uniforme (MU). Esse é o assunto tratado no vídeo abaixo.
Esse é um momento em que você estará vendo uma ligação bem estreita da Física com a Matemática (função de primeiro grau), caso não domine esse assunto de matemática, recomendo que faça uma breve revisão do conteúdo.
No vídeo seguinte continuaremos vendo mais alguns problemas de aprendizagem. A partir do próximo vídeo você deve resolver alguns problemas de relacionados ao assunto denominado movimento uniforme.
Aceleração Escalar
Conforme estudamos nas aulas anteriores, o movimento uniforme tem como característica a velocidade constante e não nula. Agora veremos o conceito de aceleração escalar. Sempre que o movimento de um objeto apresentar variação de velocidade para mais ou para menos, estará presente neste processo a grandeza física denominada aceleração, conforme veremos na aula do vídeo seguinte
Veja no vídeo seguinte alguns problemas de aprendizagem sobre aceleração escalar.
Função Horária da Velocidade no Movimento Uniformemente Variado
Nas aulas anteriores vimos um caso específico de movimento no qual a aceleração escalar permanece constante. Com base nessas informações vamos estudar agora o formalismo matemático que trada do comportamento temporal da velocidade. Com a equação obtida será possível prever a velocidade do objeto para um instante qualquer. O vídeo seguinte irá tratar, portanto, da função horária da velocidade na situação onde a aceleração é constante.
A sequência deste assunto encontra-se no post Função Horária da Posição.
Sobre o Fismat
O site www.fismat.com.br surgiu da ideia de elaborar um ambiente virtual que pudesse servir de apoio didáticos para meus alunos e aos estudantes que cursam disciplinas correlatas às que tenho ministrado. Procuramos aqui, utilizar os recursos tecnológicos disponíveis sem romper com os moldes convencionais de ensino.
Não temos nenhuma pretensão em tornar este site, um substituto das aulas presenciais, simplesmente queremos que o mesmo possa servir como um incremento à tradicional sala de aula. A expressão apoio didático que aparece logo na descrição do site na página principal, tem um significado especial neste contexto. Não é propósito do site, substituir as aulas presenciais de sua instituição de ensino, mas servir como apoio didático.

Nosso compromisso é gerar conteúdos através de vídeo-aulas, notas de aulas, e outras informações que possam ser úteis para os estudantes de Física do Ensino Médio, e as disciplinas de Física Geral do Ensino Superior. Além disso, o site apresentará sempre que possível, a Matemática como ferramenta para o auxílio do estudo de Física.
Fale Conosco
E-mail: contato@fismat.com.br
WhatsApp: +55 (38) 98003934
Inscreva-se para receber notificação de novos artigos!
Solucionando Sistemas Lineares e Equação de 2º Grau
A solução de muitos problema de Matemático, Física, Engenharias e áreas afins recaem nas questões básicas de solucionar um sistema linear ou mesmo uma equação de 2º grau. Assim sendo, apresento aqui uma planilha em Excel programada para solucionar tais problemas de maneira prática e simples. Baixe a planilha para usar em seu dispositivo offline.
Provas de Matemática do Ensino Médio
Nesta seção, apresento um número considerável de avaliações de Matemática já aplicadas por mim no Ensino Médio. Estas avaliações estão em formato .doc permitindo, portanto, a realização download e edição das mesmas. Acredito que estes arquivos possam ser úteis para estudantes e professores que atuam no Ensino Médio.
an combinatoria—–analise combinatoria—–aula_de_revisao—–aval mag—–bin de Newton2—–bin Newton2.1—–circunferencia—–COMBINATÓRIA5—–conjuntos—--derivada 2.5—–eq. modular—–Eq. pol 1.0—–eq. pol. 3—–Eq.poli—–exercícios de fisII—–força, campo e potencial—–Formulário—–func 1grau—–função de 1º g—–função—–função1.0—--função1.2—–funções1—–geo anal 2—–geo analit—–geo Analitica 2—–geo espacial 2.3—–geo plana 1.0—–geo plana—–Geo. ana 4—–geom anal 1—–geom espacial 36—–geom espacial—–geom espacial1.0—–geom plana—–geometria plana—–Hipérbole—--induçao elt—–lim e der—–lim e der1—–limite e der—–limite e derivada—–limite—–limite1.1—–log 2—–log. 2.1—–logaritimo—–logaritmo—–logaritmo_2.1—–logaritmo1—–magist 1.0—–magisterio rec—–magisterio_1—–magistério_2—–mat e fis desafio—–matriz 1.2—–matriz 1—–matriz—–matriz1.01—–matriz2.2—–matriz2—–matriz3—–MATRIZES III—–Matrizes51—–n comp e prob—–n complexos 1—–Nº complexo vest—–nº complexo—–P.A 101—–PA-—-PA1.2—–PA2—–pa3—–pg—–pol3—–poli.2—–Polinômios2.0—–pre-vestibular—–PROBABILIDADE—–prog geom—–prog. aritm—–prog. aritmatica—–prova substitutiva—–prova substitutiva2—–prova_substitutiva_2º_ano—–rec 2º ano—–rec. fin. 1º ano—–rec. final _3º ano—–rec_2º_ano_noturno—–rec_final_2º_ano—–repositiva—–simulado fechado 3º 2ªetapa—–simulado fis—–simulado mat—–Simulado—–SIMULADO-biologia—–sist lineares1.2-—-sist lineares1.3—–sist lineares1.5—–sist. lin 2.0—--sistema e arranjo—–sistema linear—–sistema—–sistema4.1—–sistemas lineares—–substitutiva log—–trig 1.0-—-trig 1.1—–trig 1.23—--trig 2.0—--trig 2.31—–trig 2.100—–trig 3.0—–trig 3.5—–trig. 2-—-trig. 3.2—–trig.2.11—–trig204—–trig233—--trig344-—-trigo 2-—-trigon.2-—-trigon.3—–trigonometria 1.2—–trigonometria 1—–trigonometria 2.1—–trigonometria 2.2—–trigonometria 2-—-trigonometria-—-trigonometria1.22—–trigonometria1—–trigonometria2 —
Potencial Elétrico
Notas de Aulas sobre Potencial Elétrico
Vídeo Aulas sobre Potencial Elétrico
Demonstração da Expressão do Potencial Elétrico Gerado por uma Linha de Carga
Consideremos na Figura abaixo uma barra fina, isolante e de comprimento $L$, uniformemente carregada eletricamente.
Lista de Exercícios sobre Potencial Elétrico
Lei de Gauss
Vídeo Aulas sobre Lei de Gauss
23.1 – Lei de Gauss (Conceitos Iniciais) – Campo Elétrico Produzido por um Fio Longo
23.2 – Campo Produzido por uma Superfície Metálica Eletrizada
Lista de Exercícios sobre Lei de Gauss
Campos Elétricos
Vídeo Aulas sobre Campo Elétrico
22.1 – Campos Elétricos Gerados por Cargas Puntuais
22.2 – Campo Gerado por um Dipolo Elétrico
Campo Elétrico Produzido por um Fio de Carga
Problemas Resolvidos
22.26
22.31
.Listas de Exercícios sobre Campos Elétricos
Na janela abaixo encontra-se a lista de problemas propostos para fixação do conteúdo estudado.
.